Piecewise Constant Hazards Calculations
Daniel Sabanés Bové
Source:vignettes/pwc_survival.Rmd
pwc_survival.RmdIntroduction
In this vignette we derive the explicit formula for the overall
survival under piecewise constant hazards. This is implemented in the
function PWCsurvOS().
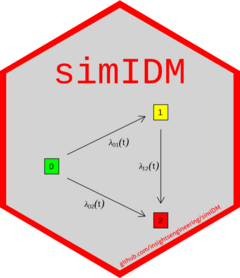
So we are in the situation where the hazards for the transitions are piecewise constant, i.e. all three hazard functions \(\lambda_{01}(t)\) (stable to progression), \(\lambda_{02}(t)\) (stable to death) and \(\lambda_{12}(t)\) (progression to death) are step functions. Say the start points of the constant hazard pieces for \(\lambda_{01}(t)\) are \(0 \equiv t_{01}^{(1)} < \dotsb < t_{01}^{(k_{01})}\), \(k_{01} \geq 1\), with corresponding constant positive hazards \(h_{01}^{(1)}, \dotsc, h_{01}^{(k_{01})}\). Obviously we use here the smallest set of pieces, i.e. neighboring hazards are required to be different, \(h_{01}^{(j)} \neq h_{01}^{(j+1)}\). This holds analogously for the hazard functions of the other two state transitions.
We denote the cumulative hazards similarly as \(\Lambda_{01}(t)\), \(\Lambda_{02}(t)\) and \(\Lambda_{12}(t)\). Note that these are piecewise linear, with the slope changes occurring at the times of hazard changes.
Overall survival calculation
Now we want to calculate the overall survival (OS) survival function induced by the piecewise constant hazard model. We start from
\[ S_{\text{OS}}(t) = S_{\text{PFS}}(t) + \int_0^t S_{\text{PFS}}(u) \lambda_{01}(u)\exp(\Lambda_{12}(u) - \Lambda_{12}(t))\, du \] where \(S_{\text{OS}}(t)\) is the survival function for OS, and \(S_{\text{PFS}}(t)\) is the survival function for PFS with the closed form
\[ S_{\text{PFS}}(t) = \exp(- \Lambda_{01}(t) - \Lambda_{02}(t)). \] Hence we can rewrite the integral from above as
\[ \exp(- \Lambda_{12}(t)) \int_0^t \exp(\Lambda_{12}(u) - \Lambda_{01}(u) - \Lambda_{02}(u))\lambda_{01}(u)\, du \] So overall we now have
\[ S_{\text{OS}}(t) = S_{\text{PFS}}(t) + \exp(- \Lambda_{12}(t)) \cal{I}(t) \] and we can rewrite the integral \[ \cal{I}(t) := \int_0^t \exp(\Lambda_{12}(u) - \Lambda_{01}(u) - \Lambda_{02}(u))\lambda_{01}(u)\, du \] in terms of the unique starting time points \(0 \equiv t_{(1)} < \dotsb < t_{(k)}\), chosen such that the set \(\{t_{(1)}, \dotsc, t_{(k)}\}\) is the smallest super set of all state specific transition starting points \(\{t_{01}^{(1)}, \dotsc, t_{01}^{(k_{01})}\}\), \(\{t_{02}^{(1)}, \dotsc, t_{02}^{(k_{02})}\}\) and \(\{t_{12}^{(1)}, \dotsc, t_{12}^{(k_{12})}\}\), as
\[\begin{align} \cal{I}(t) = &\int_{t_{(1)}}^{t_{(2)}} \exp(a_{(1)} + b_{(1)}(u - t_{(1)}))h_{01(1)}\,du \\ &+ \dotsb + \\ &\int_{t_{(l)}}^{t} \exp(a_{(l)} + b_{(l)}(u - t_{(l)}))h_{01(l)}\,du, \end{align}\] where:
- \(t_{(l)}\) is the start of the last integral part and defined as the maximum starting point that is smaller than \(t\)
- \(h_{01(j)} = \lambda_{01}(t_{(j)})\), \(j=1, \dotsc, k\) are the hazard values for the stable to progression transition within the unique time intervals
- \(a_{(j)} = \Lambda_{12}(t_{(j)}) - \Lambda_{01}(t_{(j)}) - \Lambda_{02}(t_{(j)})\), \(j=1, \dotsc, k\) are the intercepts
- \(b_{(j)} = h_{12(j)} - h_{01(j)} - h_{02(j)}\), \(j=1, \dotsc, k\) are the slopes, again using the hazard values within the unique time intervals for the specific transitions
Note that this is essentially just because of \[ \Lambda(t) = \Lambda(s) + h (t-s) \] when there is a constant hazard \(\lambda(t) \equiv h\) and two time points \(s<t\).
We can then easily derive a closed form for each integral part, \(j = 1, \dotsc, l\), where \(t_{(l+1)}\equiv t\) is the end point of the last integral:
\[\begin{align} \cal{I}_{j} &= \int_{t_{(j)}}^{t_{(j+1)}} \exp(a_{(j)} + b_{(j)}(u - t_{(j)}))h_{01(j)}\,du\\ &= \exp(a_{(j)} - b_{(j)}t_{(j)})h_{01(j)} \int_{t_{(j)}}^{t_{(j+1)}} \exp(b_{(j)}u)\,du\\ &= \exp(a_{(j)} - b_{(j)}t_{(j)})h_{01(j)} \left[ b_{(j)}^{-1}\exp(b_{(j)}u) \right]_{t_{(j)}}^{t_{(j+1)}}\\ &= \frac{h_{01(j)}}{b_{(j)}} \exp(a_{(j)} - b_{(j)}t_{(j)}) (\exp(b_{(j)}t_{(j+1)}) - \exp(b_{(j)}t_{(j)}))\\ &= \frac{h_{01(j)}}{b_{(j)}} \exp(a_{(j)}) (\exp(b_{(j)}(t_{(j+1)} - t_{(j)})) - 1) \end{align}\]
Note that if it should happen that \(b_{(j)} = 0\), the integral simplifies further to \[ \cal{I}_{j} = \int_{t_{(j)}}^{t_{(j+1)}} \exp(a_{(j)})h_{01(j)}\,du = \exp(a_{(j)})h_{01(j)}(t_{(j+1)} - t_{(j)}). \]
Implementation
The above formula is implemented in the function
PWCsurvOS(). Note that there are a few modifications
compared to above exposition:
- In order to be efficient, we look at a vector of time points \(t\) directly from the beginning. Then, find the unique time points and order them, and perform piecewise integration between the sorted unique time points.
- In order to avoid numerical overflow with large time points, we move the term \(\exp(- \Lambda_{12}(t))\) inside the integral, similarly as in the starting point of the derivation.